🎯 引言
在人工智能领域,Transformer模型已然成为了风靡全球的明星,无论是在自然语言处理、图像识别还是蛋白质结构预测等领域,它都展现了惊人的实力。然而,尽管这些模型在实际应用中表现优异,其内在的运作机制依然充满了许多未解之谜。正如某位哲人所说,”科学的进步源于发现那些看似无关紧要的小异常。” 我们的研究正是基于这样一种科学精神,发现并探讨了两种大型自回归Transformer模型(如GPT、Llama等)中普遍存在的奇异现象:
友情链接:ACEJoy
- 🚩 首个token在注意力机制中的统治地位:无论输入是什么,模型似乎都对序列中的第一个token格外“上心”。
- 🛑 隐藏状态中的异常激活值:在某些特定的特征通道中,激活值远远超出其他值,形成了“激活值巨兽”。
这些现象不仅仅是学术上的好奇心所驱动,它们在实际应用中也有重要的影响。尤其是在模型量化方面,异常激活会导致模型性能的显著下降。于是,我们提出了两种创新方法来解决这些问题:Softmax-1 和 OrthoAdam。它们不仅消除了这些现象,还提高了模型在量化过程中的鲁棒性。
接下来,让我们一起深入探讨这些现象的成因与解决方法。
🧠 第一现象:首个Token为何如此“耀眼”?
📊 现象描述
在自回归Transformer模型中,注意力机制的作用尤为关键。它决定了模型在处理每个输入时,应该“关注”哪些信息。然而,通过对多个流行的大型语言模型(如GPT-2、Llama等)进行研究后,我们发现了一个有趣且反常的现象:在98%的注意力头中,模型的查询token最关注的总是序列中的第一个token。这可真是令人费解!首个token,通常是一个特殊符号(如<bos>,表示序列开始),理论上并没有太多有价值的语义信息。那么,为什么它总是吸引着模型的“目光”呢?
🧐 原因分析
我们首先尝试排除一些可能的原因,包括位置编码、激活函数、特征归一化等。经过逐一排查,最终我们发现罪魁祸首是Softmax函数和因果掩码的结合。简而言之,由于因果掩码的存在,注意力机制必须确保每个查询token只能关注之前的key token,而第一个token是唯一一个能被所有查询token关注的key,于是它自然就成了“最受宠”的那个。
这种现象其实暗示了一种“无效注意力”现象:当某个注意力头没有找到与其相关的信息时,它便会默默地选择第一个token作为“默认选项”,这无疑浪费了模型的计算能力。
💡 解决方案:Softmax-1
针对这个问题,我们提出了一种对Softmax函数的简单改进,称为Softmax-1。其核心思想是允许注意力得分不再严格地相加为1,而是引入了一个“注意力池”,让模型可以自由选择将注意力分配到某个token,也可以选择“无处不关注”。新的Softmax-1公式如下:

通过这一改进,模型不再被迫将注意力集中在第一个token上,注意力机制得到了更大的灵活性。
🧪 实验验证
我们在GPT-2模型上进行了实验,对比了使用标准Softmax和Softmax-1的注意力图。结果显示,使用Softmax-1后,第一个token的注意力比例从之前的65%大幅下降到了3.3%。更重要的是,这一改动并没有影响模型的训练稳定性或最终性能。
graph TD; A[标准 Softmax] -->|65% 注意力| B[首个 Token]; C[Softmax-1] -->|3.3% 注意力| D[首个 Token];
🔥 第二现象:隐藏状态中的“激活值巨兽”
📊 现象描述
除了首个token的注意力问题外,我们还发现了另一个有趣的现象:在Transformer模型的隐藏状态中,在某些特定的特征通道上,激活值会异常地高出其他值几个数量级。这些“激活值巨兽”不仅仅出现在第一个token上,而是横跨整个序列,影响模型的多个层次。
这些异常激活值的存在并非只是视觉上的不美观,它们在模型的量化过程中带来了巨大的挑战。量化是一种常见的模型压缩技术,通过将模型的权重和激活值近似为较低精度的表示来减少计算开销。然而,异常激活值会扩大量化范围,从而导致非异常值的有效位数减少,进而导致模型性能的显著下降。
🧐 原因分析
通过对多种优化器的对比实验,我们发现异常激活值的出现与自适应优化器(如Adam)有着密切的关系。Adam优化器通过指数滑动平均来追踪梯度的一阶和二阶矩,这种机制在某些特定条件下会导致特定通道的激活值异常增大。
💡 解决方案:OrthoAdam
为了消除这些异常激活值,我们提出了一种全新的优化器——OrthoAdam。它的核心思想是通过正交矩阵对梯度进行变换,以避免梯度更新集中在某些特定的参数上,进而防止激活值的异常增长。OrthoAdam的算法流程如下:
Algorithm: OrthoAdam
Input: 学习率 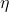 , 一阶矩衰减率
, 一阶矩衰减率 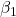 , 二阶矩衰减率
, 二阶矩衰减率 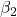 , 数值稳定项
, 数值稳定项  Output: 优化后的模型参数
Output: 优化后的模型参数 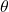 1. 初始化时间步长 t = 0,参数向量
1. 初始化时间步长 t = 0,参数向量 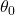 ,一阶矩
,一阶矩 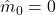 ,二阶矩
,二阶矩 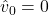 2. 随机生成正交矩阵 Q
3. Repeat until convergence:
a. 计算梯度
2. 随机生成正交矩阵 Q
3. Repeat until convergence:
a. 计算梯度 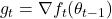 b. 应用正交变换
b. 应用正交变换 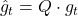 c. 更新一阶矩和二阶矩
c. 更新一阶矩和二阶矩
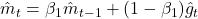
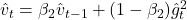 d. 计算偏差修正后的梯度
d. 计算偏差修正后的梯度 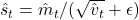 e. 将修正后的梯度变换回模型参数空间
e. 将修正后的梯度变换回模型参数空间 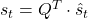 f. 更新参数
f. 更新参数 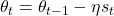
🧪 实验验证
通过使用OrthoAdam,我们成功地将异常激活值的峰度(kurtosis)从1657降到了3.1。这意味着模型的激活值分布更加均匀,极大地改善了模型的量化性能。在4位权重量化的实验中,模型的困惑度惩罚从原来的3565下降到了0.3。
pie
title 激活值峰度对比
"标准 Adam" : 1657
"OrthoAdam" : 3.1🧩 实际应用中的挑战与机遇
虽然首个token的注意力统治和隐藏状态的异常激活值看似只是理论上的问题,但它们在实际应用中会带来不少挑战。尤其是在模型量化的场景下,异常激活值会导致模型性能的大幅下降。传统的解决方案往往需要复杂的混合精度分解或是对权重和激活值的复杂缩放策略。而我们的Softmax-1和OrthoAdam方法不仅简单有效,还能让模型在最基本的量化方法下保持良好的性能。
量化实验结果
我们在GPT-2和Llama模型上测试了8位和4位量化方案,实验结果表明,使用Softmax-1和OrthoAdam的模型在量化后的性能显著优于使用传统Softmax和Adam优化器的模型。
表1: 不同模型在量化前后的困惑度对比 (PPL越低越好)
模型 | 参数量 | 量化前PPL | 8位量化PPL | 4位量化PPL
---------------|--------|----------|------------|-----------
GPT2-Small | 137M | 37.8 | 43.5 | 68.5
GPT2-Medium | 350M | 28.8 | 32.3 | 33.9
Llama2-7B | 6.7B | 7.7 | 21.5 | 19.7
GPT2 (Ours) | 350M | 16.3 | 16.5 | 17.1🔚 结论
通过对Transformer模型中两个奇异现象的深入探讨,我们提出了两个简单而有效的解决方案:Softmax-1和OrthoAdam。这些方法不仅解决了首个token的注意力统治和隐藏状态的异常激活值问题,还显著提升了模型在量化后的性能表现。我们的研究不仅为深入理解Transformer模型提供了新的视角,也为模型优化和压缩技术带来了实际的应用价值。
📚 参考文献
- Elhage, N., et al. (2022). “Transformers Revisited.”
- Dettmers, T., et al. (2022). “LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale.”
- Touvron, H., et al. (2023). “LLaMA: Open and Efficient Foundation Language Models.”
- Kingma, D. P., & Ba, J. (2015). “Adam: A Method for Stochastic Optimization.”
- Vaswani, A., et al. (2017). “Attention is All You Need.”
发表回复